Rovatok 2015-től
Rovatok
- Bemutatkozás »
- Fejlesztés beruházás »
- Informatika »
- Korszerűsítés »
- Környezetvédelem »
- Közlekedésbiztonság »
- Közlekedéstörténet »
- Kutatás »
- Megemlékezés »
- Méréstechnika »
- Mérnöki ismeretek »
- Minőségbiztosítás »
- Szabályzatok »
- Technológia »
- Egyéb »
Szerzői segédlet
A Sínek Világa folyóirat szerzőinek összeállított szempontok és segédlet.
Tovább »A polimer-kompozit hevederes ragasztott-szigetelt sínkötések (3. rész) – Véges elemes modellezések
A véges elemes modell kalibrációja és validációja
A FEM-modell kalibrációját és validációját annak használata előtt el kellett végeznünk. Ez azt jelentette, hogy például ugyanarra a terhelési állapotra (értsd: fárasztás előtti és/vagy adott fárasztási ciklust követő mérések) több mérési adatra volt szükségünk annak érdekében, hogy ki lehessen küszöbölni, illetve minimalizálni lehessen a laboratóriumi mérések által hordozott mérési hibákat a kalibráció során. Ez a több mérési adat a 600 (900)…1490 mm támaszközön mért adatsorozat volt.
A FEM-modellünk – az előző fejezetekben bemutatott módon – egy egyszerűsített 2D-s gerendamodell volt, az említett félmerev csuklóval kiegészítve. Ez azt jelentette, hogy egyetlen paraméter „beállítása” volt szükséges a kalibrációk során, ez a félmerev csukló elfordulási merevsége (αsrh) a tartó (gerenda) függőleges síkjában. Egy gerendamodell statikai kalkulációja eredményeképpen a tartó rugalmas vonalát kaptuk meg. (A többi eredményparamétert figyelmen kívül lehetett hagyni.) A kalibrációhoz a támaszközépi függőleges lehajlást használtuk fel minden támaszköz és a fárasztási ciklusszám függvényében.
 A kalibrációt iterációval lehetett minden mérési adatpárhoz illeszkedően elvégezni, ezt első körben csak „előkalibrációnak” tekintettük, és az iterációt addig végeztük, amíg az Axis VM-modellből az adott esetre a támaszközépi lehajlás ezredmilliméter-pontossággal meg nem egyezett a laboratóriumi méréseink értékeivel. Ezzel a módszerrel fárasztási ciklusonként (mindösszesen hét terhelési állapot) 13-16 darab αsrh paramétert kaptunk eredményül, amelyeket az 1. táblázatban tüntettünk fel az alábbi jelöléseket felhasználva:
A kalibrációt iterációval lehetett minden mérési adatpárhoz illeszkedően elvégezni, ezt első körben csak „előkalibrációnak” tekintettük, és az iterációt addig végeztük, amíg az Axis VM-modellből az adott esetre a támaszközépi lehajlás ezredmilliméter-pontossággal meg nem egyezett a laboratóriumi méréseink értékeivel. Ezzel a módszerrel fárasztási ciklusonként (mindösszesen hét terhelési állapot) 13-16 darab αsrh paramétert kaptunk eredményül, amelyeket az 1. táblázatban tüntettünk fel az alábbi jelöléseket felhasználva:
– fárasztás előtt (FE),
– 0,5 millió ciklusnyi fárasztást követően FU (0,5 M),
– 1,0 millió ciklusnyi fárasztást követően FU (1,0 M),
– 1,5 millió ciklusnyi fárasztást követően FU (1,5 M),
– 2,0 millió ciklusnyi fárasztást követően FU (2,0 M),
– 2,5 millió ciklusnyi fárasztást követően FU (2,5 M),
– 3,5 millió ciklusnyi fárasztást követően FU (3,5 M).
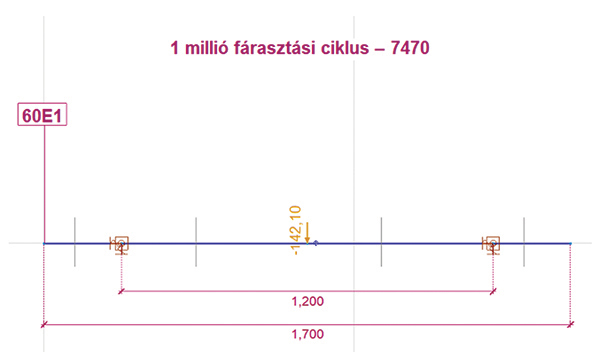 1. ábra. Sematikus, „előkalibrált” FEM-modell a ragasztott-szigetelt sínillesztések kalkulációjára 60-as sínrendszer esetén L = 1200 mm, F = -142,10 kN, FU (1 M), αsrh = 7470 kNm/rad
1. ábra. Sematikus, „előkalibrált” FEM-modell a ragasztott-szigetelt sínillesztések kalkulációjára 60-as sínrendszer esetén L = 1200 mm, F = -142,10 kN, FU (1 M), αsrh = 7470 kNm/radA modell validációját kétféle módszerrel végeztük el:
1. validációs eset: kalibráció a 2,5 milliós fárasztási ciklusú adatokkal, ezt követően validálás a 3,5 milliós fárasztási ciklusú értékekkel (azaz, hogy a megállított romlási trendfüggvény alkalmas-e előre jelezni megfelelő pontossággal egy, a kalibrálási tartományba nem beleeső értéket), valamint
2. validációs eset: a 3,5 millió fárasztási ciklusú adatsorra kalibráció az 1000…1490 mm-es támaszközök figyelembevételével, validáció a 600…950 mm-es támaszközértékekre (azaz, hogy a megállapított elfordulási merevség mennyire alkalmas a kalibrált támaszközöktől eltérő támaszközökre való átszámításra).
Az 1. táblázatban részleteztük a kalibrációhoz felhasználható adatokat. Minden esetben a kalkulált átlagértékekkel számoltunk. Természetesen meg kell jegyeznünk, hogy az 1. táblázat értékei minden esetben a laboratóriumi mérések esetleges hibáit „örökölték”, így a feltüntetett körülbelül 5-12% közötti – viszonylag magas – relatív szórásértékek is e miatt adód(hat)tak. Ezek minden esetben befolyásoló tényezőként benne lesznek a validációban, és természetesen a további kalkulációkban is.
A fárasztási ciklusszám függvényében az αsrh paraméter változása az első 0,5 millió ciklus alatt viszonylag gyors (2. ábra). A grafikonból megállapítható, hogy a 0,5…3,5 millió fárasztási ciklus közötti tartományban közel lineáris az elfordulási merevség változása.
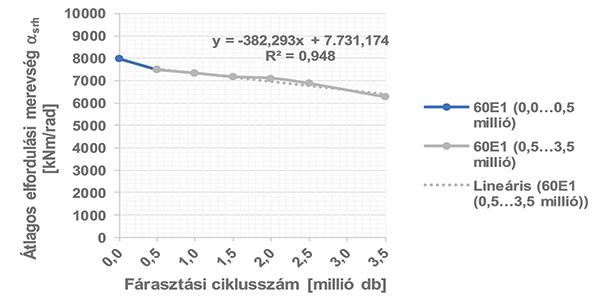 2. ábra. Az átlagos elfordulási merevség paraméter változása a 0,0…0,5 és a 0,5…3,5 millió ciklushoz tartozó fárasztási intervallumokon, 60-as sínrendszer esetében
2. ábra. Az átlagos elfordulási merevség paraméter változása a 0,0…0,5 és a 0,5…3,5 millió ciklushoz tartozó fárasztási intervallumokon, 60-as sínrendszer esetében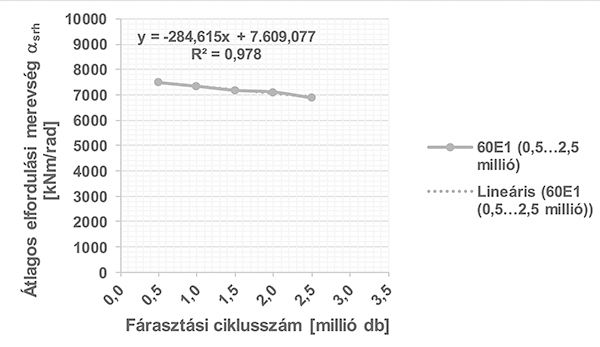 3. ábra. Az átlagos elfordulási merevség paraméter változása a 0,5…2,5 millió ciklushoz tartozó fárasztási intervallumon, 60-as sínrendszer esetében (1. validálási esethez)
3. ábra. Az átlagos elfordulási merevség paraméter változása a 0,5…2,5 millió ciklushoz tartozó fárasztási intervallumon, 60-as sínrendszer esetében (1. validálási esethez)Az 1. validációs esethez elkészítettük a 3. ábrát is, amelyen a figyelembe veendő lineáris regressziós egyenes és egyenlete látható.
Irodalomjegyzék
- [1] Németh A, Fischer Sz. A polimer-kompozit hevederes ragasztott-szigetelt sínkötések (1. rész) – Laboratóriumi vizsgálatok. Sínek Világa 2016;6:2-6.
- [2] Németh A, Fischer Sz. A polimer-kompozit hevederes ragasztott-szigetelt sínkötések (2. rész) – Vasúti pályás vizsgálatok. Sínek Világa 2018;6:12-17.
- [3] Németh A, Major Z, Fischer Sz. FEM modelling possibilities of glued insulated rail joints for CWR tracks. Acta Technica Jaurinensis 2020;13(1):42-84.
- [4] Németh A, Fischer Sz. Laboratory test results of glued insulated rail joints assembled with traditional steel and fibre-glass reinforced resin-bonded fishplates. Nauka ta Progres Transportu 2019;81(3):65-86.
- [5] Németh A, Fekete I, Szalai Sz, Fischer Sz. Supplementary laboratory investigations of modern plastic-polymer fishplates for rail joints. Nauka ta Progres Transportu 2019;84(6):86-102.
- [6] Németh A, Fischer Sz. Field tests of glued insulated rail joints with usage of special plastic and steel fishplates.
- Nauka ta Progres Transportu 2019;80(2):60-76.
- [7] https://www.researchgate.net/profile/Attila_Nemeth6/research
- [8] https://www.researchgate.net/profile/Szabolcs_Fischer/research
- [9] https://mmtdi.sze.hu/nemeth-attila
Ha szeretne rendszeresen hozzájutni a legfrisebb számokhoz, fizessen elő a folyóiratra.
