Rovatok 2015-től
Rovatok
- Bemutatkozás »
- Fejlesztés beruházás »
- Informatika »
- Korszerűsítés »
- Környezetvédelem »
- Közlekedésbiztonság »
- Közlekedéstörténet »
- Kutatás »
- Megemlékezés »
- Méréstechnika »
- Mérnöki ismeretek »
- Minőségbiztosítás »
- Szabályzatok »
- Technológia »
- Egyéb »
Szerzői segédlet
A Sínek Világa folyóirat szerzőinek összeállított szempontok és segédlet.
Tovább »A vágánygeometria romlási modelljének összehasonlító elemzése
A cikk a vasúti pálya geometriai romlási modelljeinek elemző vizsgálatával foglalkozik. Bemutat négy, egyszerűbb előrejelző alapmodellt, valamint egy lineáris és egy exponenciális regressziós modellt. Ezt követően a szerző a modellekkel készített előrejelzéseket összehasonlítja a mesterséges neurális hálózatot használó előrejelző modellel. Az eljárás célja annak bemutatása, hogy az eddig használt modellek közül van olyan, amit nagyon korlátozott kereteken belül tarthatunk alkalmasnak előrejelzésre és leírásra, van olyan, amelyik az állapot leírására tágabb keretek között is alkalmas, míg van olyan, amely az előrejelzéseket illetően a legpontosabb eredményeket szolgáltatja.
Felmerülhet a kérdés, hogy az előrejelzéseknek mekkora a szórása, mivel egy jobb átlagot hozó, de jelentősen nagyobb szórással rendelkező modell nem mondható jobb becslésnek. Így megvizsgáltam az előrejelzések szórását fél évekre lebontva, s ennek eredményeit a 9–11. ábra mutatja. Jól látható, hogy az előrejelzés szórásai között nincs szignifikáns különbség.
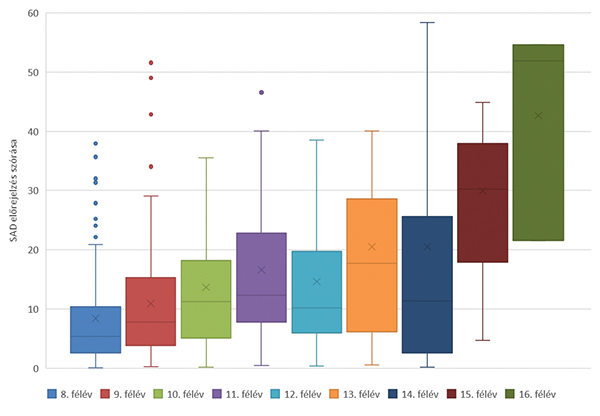 9. ábra. Alapmodell 4 előrejelzési szórásának Box Plot ábrája
9. ábra. Alapmodell 4 előrejelzési szórásának Box Plot ábrája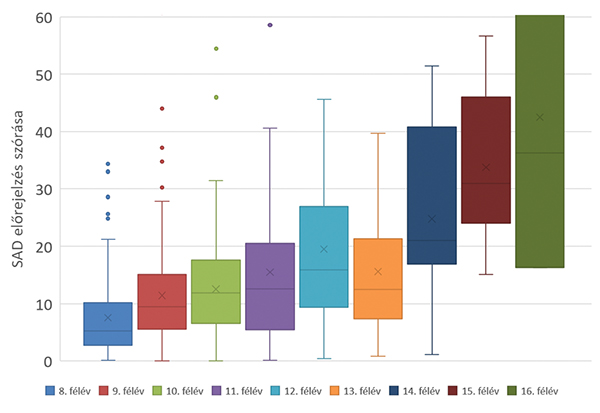 10. ábra. A lineáris regressziós modell előrejelzési szórásának Box Plot ábrája
10. ábra. A lineáris regressziós modell előrejelzési szórásának Box Plot ábrája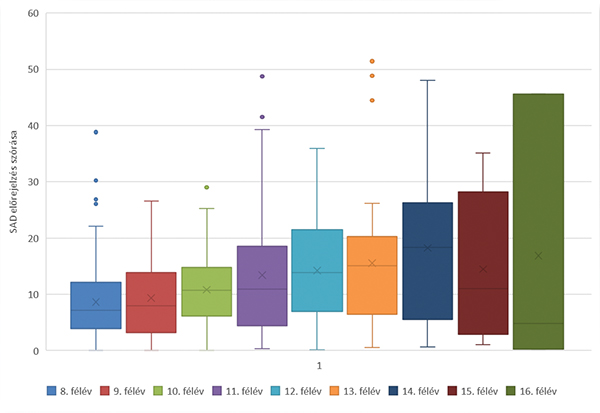 11. ábra. A mesterséges neurális hálós modell előrejelzési szórásának Box Plot ábrája
11. ábra. A mesterséges neurális hálós modell előrejelzési szórásának Box Plot ábrájaA 7. ábrán láthatóan bizonyítást nyert a 60. számú (Pécs–Gyékényes-) vasútvonal példáján, hogy a Vaszary-féle romlási egyenlet a vasúti vágány geometriai romlásának leírására alkalmas, ugyanakkor a romlás előrejelzésére nem a legpontosabb modell. Olyan eljárást kell keresni, amely a pályaállapot változásának előrejelzését a mai kor eszközeivel megbízhatóbb módon modellezi. Az itt bemutatott új modellt (mesterséges neurális hálózat) segítségül hívva belátható, hogy jelentősen jobb eredményeket ad az eddigi modelleknél. Ennek köszönhetően a vonal geometriai romlásának az átlagos előrejelzési hibáját az exponenciális előrejelzés hibájának 38%-ára tudtam csökkenteni, míg a modell abszolút hibája 27% alatti marad a 9. előre jelzett fél év esetében is.
Irodalomjegyzék
- [1] Wen M, Li R, Salling KB. Optimization of preventive condition-based tamping for railway tracks. European Journal of Operational Research Elsevier BV 2016;252(2):455-65. DOI: 10.1016/j.ejor.2016.01.024.
- [2] Mishra M, et al. Particle filter-based prognostic approach for railway track geometry. Mechanical Systems and Signal Processing. Elsevier Ltd. 2017;96:226-38. DOI: 10.1016/j.ymssp.2017.04.010.
- [3] Chiachío J, et al. A knowledge-based prognostics framework for railway track geometry degradation. Reliability Engineering and System Safety 2019;181:127-41. DOI: 10.1016/j.ress.2018.07.004.
- [4] Lasisi A, Attoh-Okine N. Principal components analysis and track quality index: A machine learning approach. Transportation Research Part C: Emerging Technologies. Elsevier 2018;91:230-48. DOI: 10.1016/j.trc.2018.04.001.
- [5] Xin T, et al. Grey-system-theory-based model for the prediction of track geometry quality. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit 2016;230(7):1735-44. DOI: 10.1177/0954409715610603.
- [6] Quiroga L, Schneider E. Modelling of high speed rail geometry aging as a discrete-continuous process. 2010
- [7] Jia C, et al. Track irregularity time series analysis and trend forecasting. Discrete Dynamics in Nature and Society, 2012. DOI: 10.1155/2012/38785
- [8] Andrade AR, Teixeira PF. Hierarchical Bayesian modelling of rail track geometry degradation. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit 2013;227(4):364-75. DOI: 10.1177/0954409713486619.
- [9] Sharma S, et al. Data-driven optimization of railway maintenance for track geometry. Transportation Research Part C: Emerging Technologies. Elsevier 2018;90:34-58. DOI: 10.1016/j.trc.2018.02.019.
- [10] Altrichter, et al. Mesterséges intelligencia elektronikus almanach. 2006
- [11] Csaji BC. Approximatino with artiificial Neural Networks. 2001
- [12] Levenberg K. A method for the solution of certain non-linear problems in least squares. Quarterly of Applied Mathematics 1944;2(2):164-8.
- [13] Marquardt DW. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. Journal of the Society for Industrial and Applied Mathematics 1963;11(2):431-41.
Ha szeretne rendszeresen hozzájutni a legfrisebb számokhoz, fizessen elő a folyóiratra.
A hozzászólások megtekintéséhez vagy új hozzászólás írásához be kell jelentkeznie!
