A számítást tizenkét Shinkansen szerelvénnyel végeztük el. Relatíve kis járműsebességig (v=36 km/h) a vasúti jármű erőkkel való modellezése és a jármű dinamikai rendszer figyelembevétele gyakorlati szempontból azonos eredményt ad (14. ábra), azonban a hídra vonatkozó rezonanciasebességnél (v=360 km/h) a dinamikai rendszer ~35%-kal kisebb hídlehajlást ad eredményül (15. ábra). Ennek oka, hogy a járműszerkezetben lengéscsillapítók dolgoznak, ezek pedig a hídszerkezet lengéseit is csökkentik. Az MSZ-EN 1991-2 6.15 ábrája éppen ezt a többletcsillapítási hatást veszi figyelembe, amennyiben csak erőkkel modellezzük a járművet. A nagy járműsebesség esetén jól látható a rezonancia kialakulása. Ennek oka, hogy az azonos járművekből összeállított szerelvény szabályos távolságonként levő erőcsoportjai ismétlődő terhelést adnak a hídszerkezetre, a rezonanciasebességnél a szerkezet sajátfrekvenciájának megfelelő gerjesztéssel. A kialakuló dinamikus tényező kiemelkedően magas, 9 körüli értékre adódik. Összehasonlításképpen meghatároztuk a teherbírásra vonatkozó dinamikus tényezőt, ami Φ2=1,14. A statikus dinamikus tényezőt az LM71 (és SW/0) terhekkel kell kombinálni, de figyelembe véve a nagyon magas számított dinamikus tényezőt, ennél lényegesen nagyobb hatást okoz a nagy sebességű szerelvény a kisebb tengelyterhek (F=136 kN) ellenére. A bemutatott dinamikai számítás a jármű dinamikus hatásának az MSZ-EN 1991-2 szerinti (6.4.1) szakaszának csak az első két részét (nagy sebességű ráhaladás és a tartószerkezet tehetetlenségi válasza miatti többlet, valamint az azonos távolságban levő tengelyek rezonanciaszerű terhelése miatti többlet) veszi figyelembe, de a jármű kerekeinek és a pálya egyenetlenségeiből keletkező hatást nem modellezi. Megjegyezzük, hogy a jármű dinamikai modellezésével nem jelent gondot a pálya adott függvénnyel felvett egyenetlenségeit is figyelembe venni [3], de ezzel jelen cikkünkben nem foglalkozunk. A parti hidaknál dinamikai vizsgálatokra a VHSz H1.2. Utasítás szerint nem volt szükség, de a szemléletesség kedvéért a vonalra nem reális járművet és járműsebességeket vettünk figyelembe. Megjegyezzük, hogy az MSZ-EN a HSLM (High Speed Load Model) tehermodellt írja elő nagy sebességek előfordulása esetén, amihez a mértékadó sebességeket és járműelrendezést az E mellékletben részletezi. A mederhíd esetében más a helyzet, mert a dinamikai vizsgálat szükségessége a nagy fesztávolság miatt nem dönthető el, emiatt az eddig ismertetett módszerekkel elvégeztük a számításokat. A dinamikai vizsgálatot a vonalszakaszra reális járművekkel (MSZ-EN 1991-2, D melléklet szerint) végeztük el. A járműveket ebben az esetben csak erőkkel modelleztük (16. ábra).

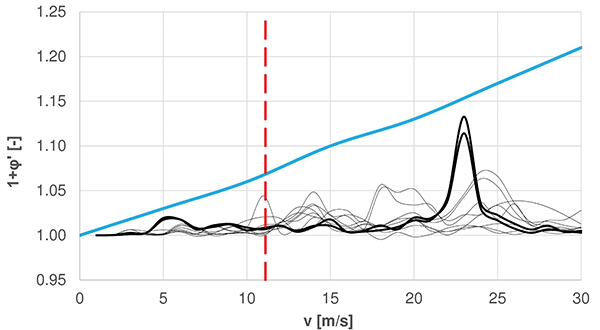
A dinamikus lehajlásokat a merevítőtartó mezőközépi keresztmetszetében és a negyedelő pontban számítottuk. Ötféle jármű áthaladása esetén (5., 6., 11. és 12. jelű tehermodellek, továbbá két M61 dízelmozdony) meghatároztuk a merevítőtartó két kitüntetett pontjának dinamikus tényezőit a járműsebességek függvényében (17. ábra). A sebesség függvényében mindegyik járműre ábrázoltuk a dinamikus tényezők eloszlásait fekete vonalakkal. Adott járműsebességeknél kiemelkedő értékek figyelhetők meg, a legnagyobb csúcsérték az 5-ös tehermodellel számolva jelentkezik v=23 m/s körül. Összehasonlításképpen ábrázoltuk az MSZ-EN 1991-2 D mellékletében előírt dinamikus tényezőt is (1+φ’) vastag kék vonallal. A jellemző hossznak a függesztőkábelek négyszeres távolságát vettük alapul, amit a hálós kábelelrendezés miatt csak becsülni lehetett (LΦ=24 m). Megjegyezzük, hogy az egyenetlenségeket is tartalmazó résszel (φ’’) kiegészített teljes dinamikus tényező a C melléklet alapján is számolható. A VHSz H.1.2. Utasításban a D mellékletet kell alkalmazni fáradásvizsgálathoz, ami a C mellékletben szereplő összefüggések egyszerűsített változatának tekinthető. A C melléklet képleteiben a jellemző hossz és sebesség mellett a szerkezet sajátfrekvenciája is szerepel a képletekben.