A felületelemekre ezt követően hőmérsékleti terhet definiáltunk. Azzal a feltevéssel éltünk, hogy a falazat egyenletesen melegszik fel, így alsó és felső felületén ugyanazt a hőmérsékleti értéket vettük alapul. Konzervatív módon minden esetben a vizsgálati hőmérsékletet (θ) megegyezőnek tekintettük a falazatra ható hőmérséklet-változással. A modellben egyéb hatást (önsúly, földnyomás) nem vettünk figyelembe. A leterhelt modellt a 7. ábra szemlélteti.
Lineáris statikai számítással váltak meghatározhatóvá az eredmények. A 8. ábra szemlélteti az alagúttengely-irányú kényszerfeszültségeket C=0,05 N/mm3 ágyazási tényező és 400 °C hőmérséklet-változás esetén. Vizsgálatunkban a maximálisan figyelembe vett hőmérséklet-változás értékét 400 °C-ban limitáltuk Reszka és szerzőtársai nyomán [18], akik 350–400 °C-ban határozták meg az öntöttvas falazatok tönkremeneteli hőmérsékletét számításaik alapján.
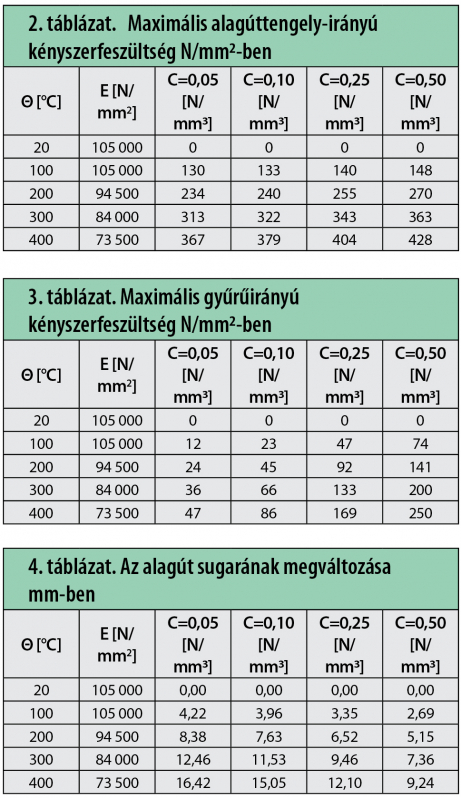
Modelljeink alapján az alábbi tényezőket határoztuk meg:

• maximális alagúttengely-irányú kényszerfeszültség (2. táblázat),
• maximális gyűrűirányú kényszerfeszültség (3. táblázat),
• az alagút sugarának megváltozása (4. táblázat).

Elvégzett vizsgálataink alapján belátható, hogy az ágyazási tényező értéke kismértékben befolyásolja az alagúttengely-irányú kényszerfeszültségek kialakulását, míg a gyűrűirányút szignifikánsan. A merevebb ágyazás minden esetben nagyobb feszültségértéket eredményez. A gyűrűirányú kényszerfeszültségek minden esetben kisebbek a hosszirányúaknál az alagútgyűrű alakváltozásának köszönhetően, amelyek értéke vizsgált modelljeink alapján akár centiméter nagyságrendű is lehet.

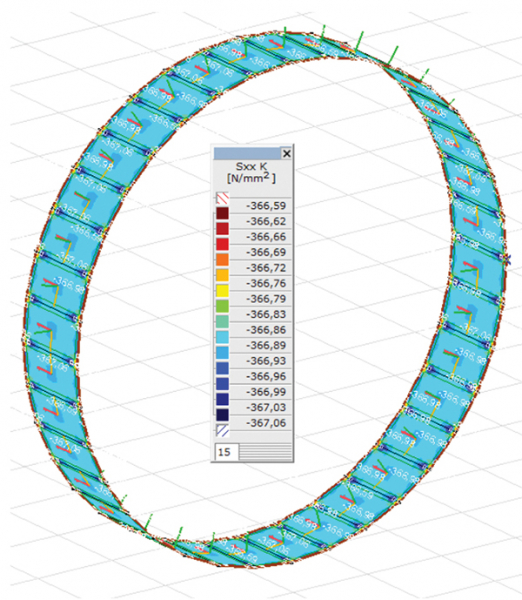
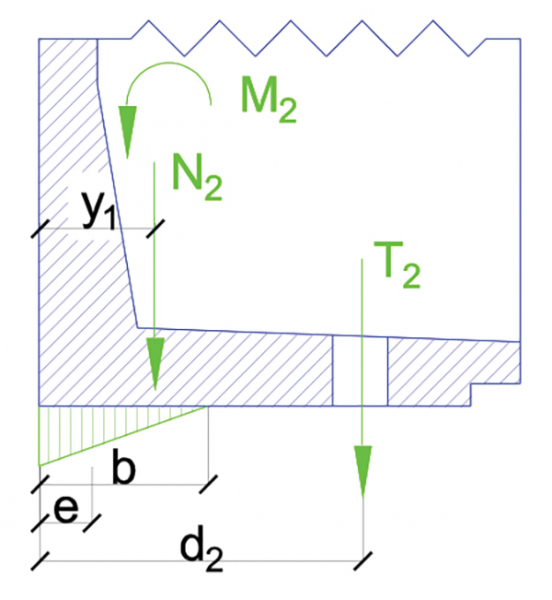
Érdekes kérdés merül fel abban az esetben, ha megfigyeljük a 2. táblázatban összefoglalt eredményeket. Ezeket az alagúttengely-irányú kényszerfeszültségeket csak a 9. képlet szerint kell vizsgálni, nem szükséges a többi terhelés hatásának vizsgálata. Látható, hogy a nyomószilárdság alapértékeként tűzhatás során figyelembe vett 140 N/mm2 értéke már 100 °C hőmérséklet-változás esetén is kimerülhet, szemben a Reszka és szerzőtársai [18] által közölt 350–400 °C-kal. Ez az ellentmondás felkeltette érdeklődésünket és a Városi földalatti műtárgyak tervezése és kivitelezése című könyvben [5] érdekes adatokra bukkantunk. E szerint míg hazánkban a korábban ismertetett szürke vasöntvényt alkalmazták, addig az NSZK-ban és Ausztriában a nagyobb szilárdságú és rugalmasságú gömbgrafitos öntvények alkalmazása is megjelent, amelyek a hazai 180 N/mm2 szakítószilárdsággal szemben 500 N/mm2 szakítószilárdsággal rendelkeztek, azaz sokkal nagyobb kényszerfeszültségek kialakulását teszik lehetővé, ami nagyobb tönkremeneteli hőmérsékletet eredményez.

Megjegyzés: A kényszerfeszültségek alakulására a csavarok lokális vízszigetelése is hatást gyakorolhat, amely kilágyulása révén némiképp csökkentheti annak értékét.