2. Minden zóna középvonalában meghatározandó a beton fajlagos hosszváltozása (εc,i[θc,i]), amelynek felvételét cikksorozatunk 1. része [1] alapján lehet megtenni. Analóg módon, ahogy azt az öszvér szerkezetek számítása során is tesszük, feltételezzük, hogy azt az alakváltozást az alagútfalazat 100%-ban meggátolja és így abban igénybevételek ébrednek. Megjegyezzük, hogy pontosabb számítási igény esetén az alagútfalazat mozgásának figyelembevételével az igénybevételek mérsékelhetők.

3. Meghatározandó minden zóna középvonalában a beton rugalmassági modulusa (Ec,θ,i). Ennek felvétele során a 23. képletnek megfelelően a szobahőmérsékleten értelmezett értéket (Ec) módosítottuk egy csökkentő tényezővel (φc,θ) a 23. képletnek megfelelően. A csökkentő tényező értékét az φc,θ és εc,1,θ értékek által meghatározott húrmodulus megváltozásával vettük figyelembe a 24. képletnek megfelelően a 20. ábra alapján (kék színű vona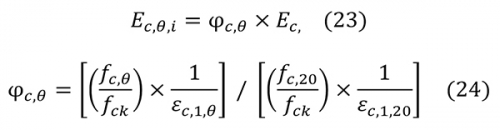l).
ahol:
Ec,θ,i: a beton rugalmassági modulusa az egyes zónákban,
φc,θ: a rugalmassági modulust módosító tényező θ hőmérsékleten,
Ec: a beton rugalmassági modulusa normálhőmérsékleten,
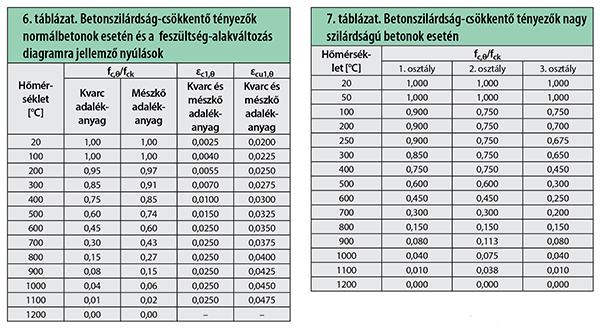
(fc,θ/fck): a beton nyomószilárdságának csökkentő tényezője θ hőmérsékleten (lásd 6. és 7. táblázat),
εc,1,θ: a beton feszültség-alakváltozás diagramjára jellemző érték θ hőmérsékleten (lásd 6. táblázat),
(fc,20/fck): a beton nyomószilárdságának csökkentő tényezője 20 °C hőmérsékleten (lásd 6. és 7. táblázat),
εc,1,20: a beton feszültség-alakváltozás diagramjára jellemző érték 20 °C hőmérsékleten (lásd 6. táblázat).
4. Meghatározandó minden zóna középvonalában a kialakuló hőmérsékleti kényszerfeszültség (σc,θ,i). Ezt a 25. képlet alapján lehet figyelembe venni. A képletben szereplő β tényező a kétirányú gátolt alakváltozás hatását veszi figyelembe a 26. képlet alapján [21].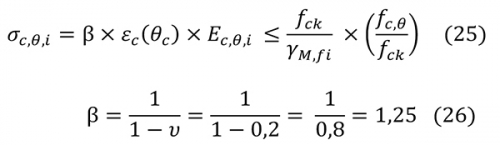


ahol:
σc,θ,i: a gátolt hőmérséklet-változás miatt kialakuló feszültség az egyes zónákban,
β: a kétirányú gátolt alakváltozást figyelembe vevő módosító tényező,
Ec,θ,i: a beton rugalmassági modulusa az egyes zónákban,
fck: a beton nyomószilárdságának karakterisztikus értéke,
γM,fi: az anyagjellemzőhöz tartozó parciális biztonsági tényező tűzhatás esetén,
(fc,θ/fck): a beton nyomószilárdságának csökkentő tényezője θ hőmérsékleten (ld. 6. és 7. táblázat),
ν: a beton Poisson-tényezője (ν=0,2).
5. Az egyes zónákban kialakuló kényszerfeszültség értékét a zóna keresztmetszeti területével (Ai) szorozva meghatározható a zónában kialakuló részerő (Fc,i). Majd ezeket összegezve a redukált keresztmetszetre ható nyomóerő (Nc). A számítást a 27. és 28. képlet ismerteti.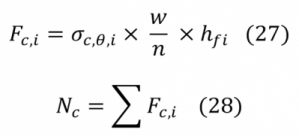


ahol:
Fc,i: a gátolt hőmérséklet-változás miatt kialakuló részerő az egyes zónákban,
σc,θ,i: a gátolt hőmérséklet-változás miatt kialakuló feszültség az egyes zónákban,
w: az alagútfalazat vastagsága,
n: az alkalmazott zónák száma,
hfi: a redukált keresztmetszet magassága,
Nc: a redukált keresztmetszetre ható nyomóerő.
6. Az egyes zónákban kialakuló részerők nyomatékát meghatározzuk a redukált keresztmetszet súlypontjára (Mc,i). A súlypont helyét a redukáltbeton-keresztmetszet súlypontjával azonosítjuk, elhanyagolva a vasalás hatását. A semleges tengelytől az alagútfalazat belső oldaláig mért távolságokat pozitív, míg a kőzet irányába mérteket negatív előjellel kell figyelembe venni. Az egyes résznyomatékok összegzésével előállítható a redukált keresztmetszetre ható nyomaték (Mc). A számítást a 29. és 30. képlet ismerteti.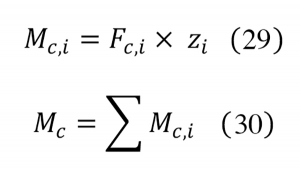
ahol:
Mc,i: a gátolt hőmérséklet-változás miatt kialakuló résznyomaték az egyes zónákban,
zi: a redukált keresztmetszet súlypontjának távolsága az egyes zónák súlypontjától,
Mc: a redukált keresztmetszetre ható nyomaték.
7. A kapott igénybevételt (N-M értékpárt) összegezzük a külső hatásokból kapott igénybevételekkel. Megjegyezzük, hogy az alkalmazott közelítéseink alapján ezek az igénybevételek nemcsak gyűrűirányban, hanem alagúttengely-irányban is kialakulnak és mindkét irányban ellenőrizendő az alagútfalazat ezekere.
8. Az összegzett igénybevételeket ellenőrizzük a keresztmetszetre jellemző egyszerűsített teherbírási vonal alapján. A teherbírási vonal szerkesztésének módját a terjedelmi korlátok miatt nem ismertetjük a tűzhatás során. Könyvünkben [9] ezt bemutatjuk, de felhívjuk a figyelmet arra, hogy az alagútfalazatok esetén a nyomatéki ábra előjelváltása miatt a falazat húzott és nyomott oldala helyet cserélhet az egyes keresztmetszetekben, így két teherbírási vonal megszerkesztése szükséges az ellenőrzés elvégzéséhez.

Összefoglalás

Cikkünk negyedik részében az elméleti megfontolások alapján a mindennapi gyakorlat számára adtunk kiindulási alapot az alagútfalazatok tűzvédelmi tervezéséhez. A korábbi részekhez hasonlóan most is külön kezeltük a fém- és betonanyagú alagútfalazatok kérdéskörét. Bemutattuk mindkét esetben a falazat merevségének megváltozását, amely döntően befolyásolja a külső hatások miatt ébredő igénybevételek alakulását. Közelítő modellek alkalmazásával bemutattuk a gátolt hőtágulásból származó igénybevételek nagyságrendjét és figyelembevételének lehetőségeit. Az igénybevételek számítását követően minden esetben bemutattuk a tartószerkezeti számítást, amellyel a tűzhatás során a szerkezet igazolása elvégezhető.
Cikkünk ötödik, záró részében az alagúttüzek teljesítményalapú vizsgálatával fogunk részletesen foglalkozni, amelyben nem csak az üzemszerű használat során kialakuló tüzek vizsgálatára fókuszálunk, hanem bemutatjuk az építés/fenntartás során keletkező tüzek számszerűsítésének módját is.