Célszerű módon elsőként a felmelegedési és a lehűlési szakasz alatti területet kell meghatározni, és majd ezek ismeretében lehet az állandósult szakasz alatt a számítást elvégezni. Az állandósult szakasz alatti részterületet a teljes terület és a két, korábban meghatározott részterület különbségeként lehet számítani.
A felmelegedési szakasz másodfokú parabolával jellemezhető, ahogy azt a 12. képlet is szemlélteti. Ebben az esetben a parabola alatti terület nem lesz más, mint a bennfoglaló téglalap területének egyharmad része. Ezt fejezi ki a 15. képlet.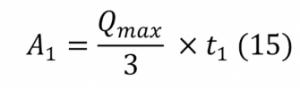

ahol:
A1: a felmelegedési szakasz alatti ábraterület [J],
Qmax: a tűz maximális hőkibocsátása [W],
t1: a felmelegedési szakasz vége [s].
A lehűlési szakaszban tudjuk, hogy a tűzteher 30%-a fog elégni, ahogy azt a 16. képlet is szemlélteti. Illetve tudjuk azt is, hogy a háromszög alakú ábraterület megegyezik a bennfoglaló téglalap területének ½ részével, amely összefüggést a 17. képlet írja le. A két függvény bal oldala A3 értékű, így a két függvényt egyenlővé téve a 18. képletet kapjuk. Ezt rendezve a 19. képlet alapján meghatározható a Δt2-érték, azaz a lehűlési szakasz hossza (a t2 és t3 időpontok között értelmezve).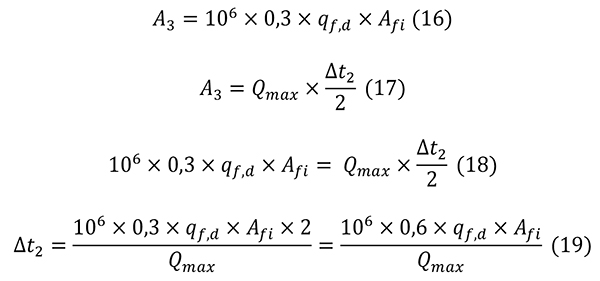

ahol:
A3: a lehűlési szakasz alatti ábraterület [J],
Afi: a lokális tűz alapterülete [m2],
qf,d: a fajlagos tűzteher tervezési értéke [MJ/m2],
Qmax: a tűz maximális hőkibocsátása [W],
Δt2: a lehűlési szakasz hossza [s].
Megjegyzés: A fellelhető szakirodalomban a lehűlési szakasz gyakran parabolikus, ha ennek feltételezésével él a tervező, akkor ugyanúgy tudja a számítást elvégezni, mint ahogy azt a felmelegedési szakasz esetén bemutattuk.
A teljes tűzteher megegyezik a grafikon alatti ábraterület értékével, amely három részterület összegeként írható fel a 20. képlet segítségével. Az állandósult szakasz alatti A2 részterület a 21. képlet alapján határozható meg. Mivel tudjuk, hogy négyszög alakú az ábraterület, így értéke a 22. képlet alapján is számításba vehető. A két egyenletet egyenlősége miatt átírhatjuk a 23. képlet szerinti formába. Ezt rendezve a 24. képlet alapján meghatározható a Δt1-érték, vagyis az állandósult szakasz hossza (a t1 és t2 időpontok között értelmezve).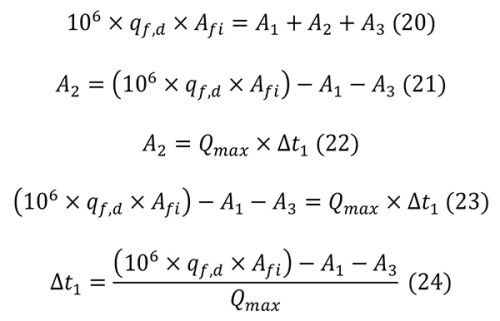

ahol:
A1: a felmelegedési szakasz alatti ábraterület [J],
A2: az állandósult szakasz alatti ábraterület [J],
A3: a lehűlési szakasz alatti ábraterület [J],
Afi: a lokális tűz alapterülete [m2],
qf,d: a fajlagos tűzteher tervezési értéke [MJ/m2],
Qmax: a tűz maximális hőkibocsátása [W],
Δt1: az állandósult szakasz hossza [s].
A Δt1- és Δt2-érték ismeretében a grafikon t2 és t3 időpillanata számíthatóvá válik a 25. és 26. képletek alapján.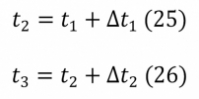

ahol:
t1: a felmelegedési szakasz vége [s],
t2: az állandósult szakasz vége [s],
t3: a lehűlési szakasz vége [s],
Δt1: az állandósult szakasz hossza [s],
Δt2: a lehűlési szakasz hossza [s].
Abban az esetben, ha a tűzhatást szellőzés határozza meg, a Qmax-értéket csökkenteni kell. Csökkentett értékére a szabvány [5] a 27. képlet szerinti egyszerűsítést is megengedi.

ahol:
Qmax,lim: a maximális hőkibocsátás csökkentett értéke [W],
Av: falakon lévő nyílások összfelülete [m2],
heq: az összes, falon elhelyezkedő ablak magasságának súlyozott átlaga [m],
Hu: a fa névleges fűtőértéke 17,5 MJ/kg értékkel figyelembe véve,
m: az égési tényező 0,8 értékkel figyelembe véve.