A láng vízszintes hossza a 35. képlet alapján vehető számításba.

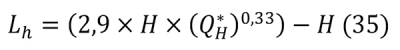ahol:
H: a tűz forrása és a födém alsó síkja közötti távolság [m],
Lh: a lokális tűz lángjának vízszintes hossza [m],
Q*H: a tűzszakasz H magasságához tartozó hőkibocsátási együttható [-].
Q*H értéke a 36. képlet alapján számítható.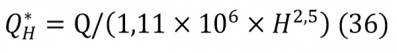

ahol:
H: a tűz forrása és a födém alsó síkja közötti távolság [m],
Q: a tűz hőkibocsátása [W],
Q*H: a tűzszakasz H magasságához tartozó hőkibocsátási együttható [-].
A virtuális hőforráshoz képest mért helykoordináta a 37. képlet szerint határozható meg.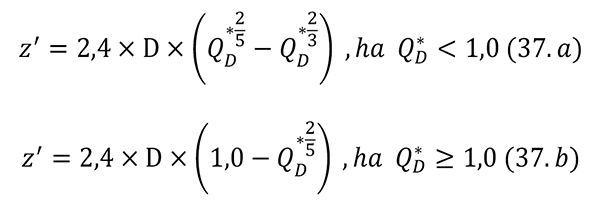

ahol:
z’: a virtuális hőforráshoz képest mért helykoordináta [m],
D: a tűz átmérője [m],
Q*D: a lokális tűz D átmérőjéhez tartozó hőkibocsátási együttható [-].
Q*D értéke a 38. képlet alapján számítható.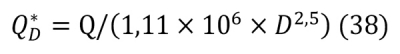

ahol:
D: a tűz átmérője [m],
Q: a tűz hőkibocsátása [W],
Q*D: a lokális tűz D átmérőjéhez tartozó hőkibocsátási együttható [-].
Hasemi módszerének nagy előnye, hogy több, egymástól elkülönített lokális tűz hatását is képes számszerűsíteni. Ez a tulajdonsága rendkívül jól alkalmazható például fedett parkolóházak tűzvédelmi tervezése során is. Ilyen vizsgálat esetén a födém alsó síkján értelmezett teljes hőáram értéke az egyes lokális tüzekből származó hőáramok összege alapján határozható meg a 39. képlet alapján.

ahol:
htot: a teljes hőáram [W/m2],
h1: az 1 jelű lokális tűzből származó hőáram [W/m2],
h2: a 2 jelű lokális tűzből származó hőáram [W/m2].
A mennyezet szintjén a tűznek kitett, egységnyi felületre érkező ténylegesen elnyelt hőáram a 40. képlet alapján számítható.

ahol:
hnet: az egységnyi felületre jutó ténylegesen elnyelt hőáram [W/m2],
h: az egységnyi felületre jutó hőáram [W/m2],
αc: a konvekciós hőátadás együtthatója [W/m2K],
Θm: a szerkezeti elem felületének hőmérséklete [°C],
σ: a Boltzmann-állandó [W/m2K4],
Φ: az elrendezési tényező [-],
εm: a szerkezeti elem felületének emissziós tényezője [-],
εf: a tűz emissziós tényezője [-].
Az egyes paraméterek értéke a következő:

• egyszerű tűzmodell esetén: αc= 35 W/m2K [5],
• konzervatív közelítésként Φ=1,0 és εf=1,0 értékű,
• a Boltzmann-állandó értéke 5,67×10-8 W/m2K4,
• εm=0,8 értékű az [5] alapján, amennyiben a tartószerkezeti szabványok másképp nem rendelkeznek.

A szabvány ezen a ponton elengedi a tervező kezét, és magára hagyja a probléma kezelésével. Ahhoz, hogy a tervezési feladatot meg tudja oldani, meg kellene tudnia határozni a Θm-értéket, amelynek módjáról a szabvány már nem rendelkezik. A kérdés megoldása során abból a feltevésből indultunk ki, hogy a szerkezeti elem nyeli el a födémre ható teljes hőáramot. Ebben az esetben hnet értéke zérus, ahogy azt a 41. képlet szemlélteti. Rendezve az egyenletet, a 42. képlet szerinti összefüggést kapjuk.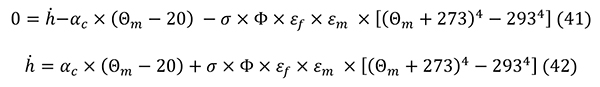

A 42. képletben Θm értéke °C-ban értelmezett. A könnyebb kezelhetőség érdekében áttérünk K-ben történő számításra, így az egyenlet a 43. képlet szerinti alakot ölti.