Bevezetés

A hézagnélküli vágány állékonysága alapvető vasútbiztonsági kérdés és számos pályaszerkezeti követelményt kell teljesíteni a kivetődés jelenségének elkerülése érdekében. A sínszálak hőmérsékletének nyári, tartósan erős napsütéses napokon bekövetkező jelentős emelkedése bennük nagy nyomóerő-növekedést okoz, amely az íves vágány erőteljes deformációját képes okozni. Ezzel az erővel szemben megbízható nagyságú ellenállásra van szükség az állékonysághoz, amit a vágány mint keretszerkezet és az ágyazat oldalirányú ellenállása képes biztosítani. Az ellenállásoknak a hatásokkal szembeni megfelelőségét számítással lehet igazolni. Elsősorban német nyelvű szakanyagokban az úgynevezett Meier-féle képletek a használatosak, létezik azonban egy kevésbé alkalmazott eljárás is, amelynek megalkotója Nemesdy Ervin, egykori műegyetemi professzor volt. Joggal vethető fel a kérdés, miben hasonlít, illetve különbözik a két módszer egymástól, és vajon az eredményeik – kvázi azonos kiinduló feltételek mellett – mennyire térnek el egymástól.
A hézagnélküli vágány állékonyságának kutatása már a múlt század harmincas éveiben megkezdődött, de igazán lendületet az 1960-as években elvégzett pályakísérletek eredményei nyomán kapott. Ezért az előzmények tárgyalása során vissza kell nyúlni több évtizedes forrásokhoz is, ismertetésüknél megtartva az eredeti, a mai mértékegységrendszertől eltérő dimenziókat, közölve az átváltott értékeket is.
A vasúti vágány rugalmasan ágyazott és oldalirányban is rugalmasan megtámasztott síkbeli tartószerkezet. A záróhegesztés elkészítésekor érvényes sínhőmérséklet emelkedésével egyre nagyobb nyomóerő alakul ki a sínszálakban, amelynek számítási kifejezése a következő:

Fhő = a sínszálban keletkező hőmérsékleti nyomóerő [N],
α = a sínacél lineáris hőtágulási tényezője [1,2×10-5 1/°C],
E = a sínacél rugalmassági modulusa [2,1×105 N/mm2],
A = a sínszál keresztmetszeti területe [mm2],
ΔT = a sín hőmérsékletének változása [°C].
A semleges hőmérséklet alsó határán (+15 °C-on) történő záróhegesztés és maximális +60 °C-os sínhőmérséklet esetén a nyomóerő nagysága egy 60E1 rendszerű sínszálban 870 kN. A vágányban ennek az erőnek kétszerese, azaz 1740 kN ébred.
Minél kisebb a vágány ívsugara, annál nagyobb a hőerő (aktív erő) ívből kifelé mutató komponense, amellyel szemben gátlóhatások dolgoznak, a vágány alakváltozással szembeni ellenállása és az ágyazat oldalirányú ellenállása. Amikor a passzív hatások nem elégséges nagyságúak, akkor bekövetkezik a kinyomódás, a kivetődés, amelynek során a vágány szabálytalan alakot vesz fel, megnövekszik a sínszálak hossza és bennük lecsökken a nyomóerő értéke. A kialakuló szabálytalan vágánygeometria kisiklást okozhat.
A vágány alakváltozással szembeni ellenállását az elméletek kétféleképpen veszik figyelembe. Az első esetben, a Meier-féle módszerben, a vágány egészének hajlítással szembeni ellenállását a helyettesítő tehetetlenségi (inercia-) nyomaték jellemzi, amelynek nagysága, függetlenül a vágány állapotától, azonos értékűnek veendő fel. A másik, a Nemesdy-féle módszer a sínszálak hajlítási ellenállásával és a sínleerősítéseknél jelentkező elforgási ellenállással számol.
A cikk a vasúti járművel nem terhelt vágány eseteire vonatkozik.

A Meier-féle számítási módszer

Dr. Meier vezette le energiamódszerrel 1937-ben a kritikus fekvéshiba húrmagasság-számítását egyenes és íves vágány esetére. A következőkben a módszer legfontosabb lépései olvashatók az [1] irodalomból átvéve. A nyomott vágányszakasz deformálódott rajza az 1. ábrán látható.
A deformációs vonal egyenlete: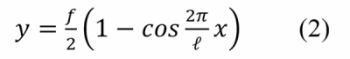

A külső erők munkája (WF) hozza létre a tartóban felgyülemlő energiát (WE+Wq), így

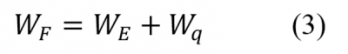Az összes munka:

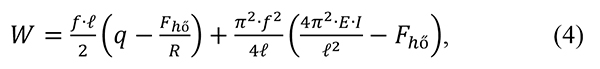ahol
f = fekvéshiba húrmagassága [mm],
x = húrhossz ≈ ℓ=ívhossz [mm],
q = oldalirányú ágyazat-ellenállás [N/mm],
Fhő = hőerő [N],
R = ívsugár [mm],
E = sínacél rugalmassági modulusa [N/mm2],
I = vágánymező tehetetlenségi nyomatéka [mm4].
A valóságos erőket helyettesítő és az x=ℓ/2 pontban a vágánytengelyre merőleges erők munkája: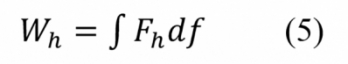

A valóságos erőket helyettesítő, az x=ℓ/2 pontban a vágánytengelyre merőlegesen ható erő:

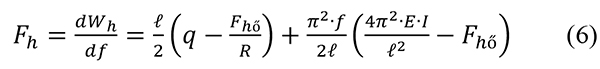Kritikus esetben: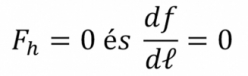

A kapott számítási kifejezések íves vágány esetére a következőkben részletezettek.

Kritikus hőmérséklet-emelkedés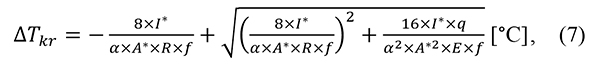

ahol    
I* = a vágány oldalirányú helyettesítő inercianyomatéka [m4],
A* = a két sínszál együttes keresztmetszeti területe [m2].

Kritikus nyomóerő a vágányban

Kritikus fekvéshiba-amplitúdó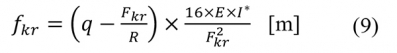

Kivetődés hossza

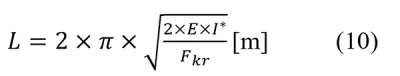Az egyes számítási kifejezések bemenő adatainak áttekintésekor megállapítható, hogy egyetlen paraméter értéke az, amelynek nagysága bizonytalanságokkal lehet terhes, ez pedig a vágány oldalirányú helyettesítő inerciája. Ezért a következőkben ezt részletesen szükséges tárgyalni. (Az oldalirányú ágyazat-ellenállás értéke nagyszámú pályakísérlet eredményei alapján megbízhatóan áll rendelkezésre.)