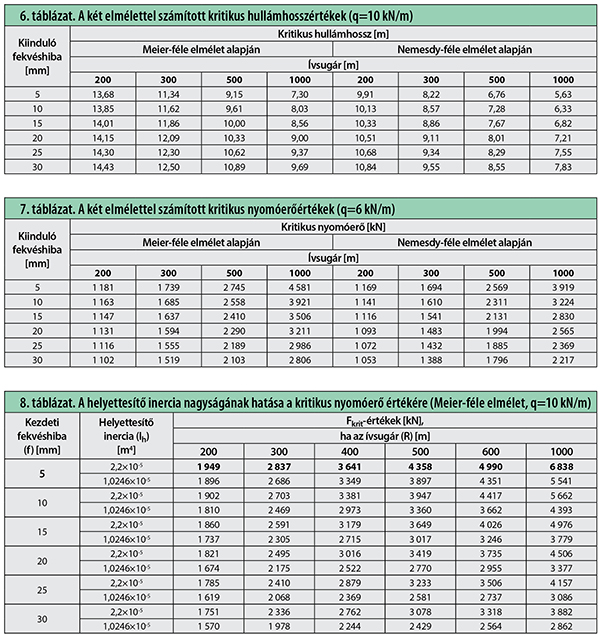
13. ábra és 6. táblázat: R=200 m sugár és f=5 mm fekvéshiba-amplitúdó esetén a Meier-féle kritikus hullámhossz 1,38-szor nagyobb, mint a Nemesdy-féle érték. Az arány R=2000 m sugár és f=30 mm fekvéshiba esetén 1,22-ra csökken.
A 7. táblázatban a két elmélettel a q=6 kN/m ágyazati oldalellenállás esetével számított kritikus nyomóerőértékek vannak összefoglalva.
R=200 m sugár és f=5 mm fekvéshiba-amplitúdó esetén a Meier-féle kritikus nyomóerő 1,01-szor nagyobb, mint a Nemesdy-féle érték. Az arány R=1000 m sugár és f=30 mm fekvéshiba esetén már 1,27.
A fentiek szerint esetenként jelentős értékeltérések adódnak az egyes számított kritikus jellemzők egymásnak megfelelő értékei között. Ez arra vezethető vissza, hogy a keretmerevség hatása a vágány oldalirányú helyettesítő inerciája által hangsúlyosabb figyelembevételt jelent a Meier-féle számításokban, mint a Nemesdy-féle módszerben az elforgás-ellenállásé.
Nézzük meg, hogy a Meier-féle elméletben a keretmerevségi hatás hogyan növeli meg a kritikus nyomóerő értékét. A 8. táblázatban a 60-as rendszerű vágánymezőre a [7] irodalom szerinti inerciával (I*=2,2×10-5 m4), illetve a két sínszál inerciaösszegével (2E.Iy=1,0246×10-5 m4) számított értékek láthatók. Az inerciák és így a keretmerevségi hatások aránya 2,15. A többi adat azonos a korábban közöltekkel.
A 8. táblázati értékek azt mutatják, hogy míg R=200 m sugarú ív oszlopában a kétféle helyettesítő inerciával számított kritikus nyomóerők aránya nem haladja meg az 1,12 értéket, addig az ívsugár és a kezdeti fekvéshiba-amplitúdó értékének növekedésével egyre nagyobb lesz a hányados és R=1000 m ívsugár és f=30 mm fekvéshiba-amplitúdó értéknél már 1,36-ra nő.

A következő lépésben „emeljük ki” a Meier-féle és a Nemesdy-féle módszer kifejezéseiből a keretmerevség hatását és nézzük meg, ebben az esetben milyen lesz a kritikus értékek viszonya. Tehát mindkét elmélet szerinti számításokban csak a két sínszál y tengelyre vett inerciájának összegével dolgozunk, amely 2Iy=1,0246×10-5 m4 nagyságú, a Nemesdy-féle kifejezésekből pedig kimarad a 2r/k tag. A többi adat azonos a közölt kiinduló értékekkel.
A kétféle elmélet alapján, a keretmerevséget nem figyelembe vevő módon, végzett számítások q=10 kN/m, illetve q=6 kN/m ágyazati oldalellenállás esetében tökéletesen megegyező értékeket adtak a kritikus nyomóerőre a paraméterek vizsgált értéktartományában (9. táblázat). Azonos a helyzet a kritikus hőmérséklet-emelkedés értékei tekintetében is, míg a kivetődési hullámhossz esetében minimálisak az eltérések.
A 14. ábra R=300 m sugarú ív, r=40 kNm/rad és q=10 kN/m értékek esetére mutatja a kritikus nyomóerő alakulását a fekvéshiba-hullámhossz függvényében, különböző fekvéshiba-amplitúdókra, a Nemesdy-féle elmélet szerint.
A Nemesdy-féle elmélet 19. képlete lehetővé teszi, hogy megvizsgáljuk, az egyes tagok, azaz a sínmerevség, az elforgás-ellenállás és az ágyazat-ellenállás milyen arányban járulnak hozzá a kritikus erő értékéhez, illetve mit okoz az elforgás-ellenállási állandó értékének változtatása. A példában R=300 m-es ív, f=20 mm nagyságú fekvéshiba szerepel és egyes hullámhosszértékekhez történik az eredmények megadása (10. táblázat). A kiinduló adatok (sínrendszer, ágyazat oldalirányú ellenállása, aljtávolság) nem változtak.

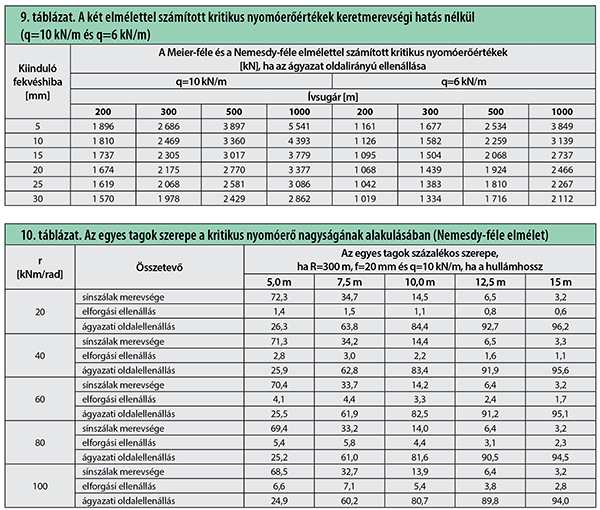
A 10. táblázat értékei alapján megállapítható, hogy közvetlen rugalmas sínleerősítések alkalmazása esetén a Nemesdy-féle elméletben a sínelfordulási állandónak van a legkisebb szerepe a kritikus erő nagyságának alakításában. A két sínszál merevsége felépítményi rendszerenként állandó érték, de hatásuk változó jelentőségű. Igen fontos a zúzottkő ágyazat mérete, fenntartottságának minősége, hogy az oldalirányú ellenállás mindig megfelelő nagyságú legyen.      

Összefoglaló megállapítások

A hézagnélküli vágány állékonysága alapvető vasútbiztonsági kérdés. A kivetődés elleni biztonság számítására két jól ismert módszer létezik, az úgynevezett Meier-féle elmélet képletei, illetve a hazai fejlesztésű eljárás, amely Nemesdy Ervin, egykori műegyetemi professzor nevéhez fűződik. A cikkben nagy vonalakban közöltük mindkét módszer elméleti alapjait. A kritikus jellemzők (kivetődést okozó nyomóerő és hőmérséklet-változás) számításánál a két elmélet abban különbözik, hogy hogyan veszi figyelembe a vágánynak a sínszálak és keresztaljak összekapcsolásából származó keretmerevségi hatását. A helyettesítő vágányinercia, illetve a sínleerősítések elforgás-ellenállási állandójának értéke számos körülménytől függ és a rendelkezésre álló szakirodalmi adatok általában nem közlik mindazon paraméterek értékeit, amelyek befolyásolják a jellemzők nagyságát. Ezért az értékek megválasztásánál nagy körültekintéssel kell eljárni.    
A cikkben ismertetett eredmények és szakmai megfontolások alapján az a javaslat fogalmazható meg, hogy vágányállékonysági számításokhoz célszerűbb a Nemesdy-féle elméletet alkalmazni, a következők okán:
– A vágány szerkezeti kialakításától függő r elforgás-ellenállási állandó laboratóriumi kísérlettel könnyen meghatározható, sőt a sínleerősítés minősítő vizsgálatánál annak értéke az MSZ EN13146-2 szabvány [10] alapján végzett mérés eredménygörbéjéből egyszerűen megállapítható.
– A Meier-féle elméletben használatos helyettesítő vágányinercia értékének megállapítására nincsen egységesen elfogadott nemzetközi módszer, így a rendelkezésre álló irodalmi értékek bizonytalanságot jelentenek.
– Azonos felépítményszerkezeti kialakításra a Nemesdy-féle számítással alacsonyabb kritikus nyomóerő- és hőmérsékletváltozás-értékek adódnak, mint a Meier-féle elmélettel, így az a biztonság javára ad eltérést.