Eltérő szerkezetű vágánymezők keretmerevségének meghatározására végeztek terhelési vizsgálatokat a Zürichi Egyetemen (ETH Zürich) [6]. A vágánymező 12 m hosszú volt, a keresztaljak alátámasztásánál a súrlódást minimalizálták. Négypontos hajlítást (két aktív és két támaszerővel) hajtottak végre, a támaszköz 10,2 m, a szimmetrikusan elhelyezett két aktív erő (maximum 10–10 kN) támadáspontjának távolsága 4,2 m volt. A terheléseket 100 mm maximális kihajlásig végezték, 30 mm-nél tehermentesítést alkalmaztak.   Megállapították, hogy a vágánymező többszörös fel-le terhelése során a mezőközépen bekövetkező azonos alakváltozásnál mért elmozdulásértékek csekély eltérései oda vezethetnek, hogy a hajlító és a nyíró alakváltozás aránya megváltozik.
A vizsgálatok során tapasztaltak szerint a vágánymező nem lineárisan rugalmas alakváltozási viselkedést mutatott. A rugalmas alakváltozások mellett – a felépítményváltozattól függően – a deformáció mintegy fele képlékeny volt, amit a sínleerősítéseknél kialakuló elcsúszások és elcsavarodások okoztak. Tehát nem volt kezdeti lineárisan rugalmas alakváltozási szakasz, amint az például az acél esetében ismert, s amely alapján a hajlítási és nyírási merevség egyszerűen kiszámítható lett volna. A különböző paraméterek merevségre gyakorolt hatásának összehasonlításakor a tiszta merevségi értékek nehezen értékelhetők a hajlítási és a nyírási merevség közötti kapcsolat alapján.
Végül elméleti megfontolások alapján felállított összefüggést használva az alábbi merevségi értékeket határozták meg 0,6 m távolságban lévő B91 vasbeton aljakkal, Skl 1 leszorítókengyelekkel szerelt vágánymezőre, ahol a csavarmeghúzási nyomaték 250 Nm volt:
– 46E1 rendszerű sínszálakkal 2302 kNm2,
– 54E2 rendszerű sínszálakkal 2206 kNm2.    
Érdekes a végeredmény, mert az 54E2 profil körülbelül 17%-kal nagyobb keresztmetszetű, mint a 46E1 profil, míg a tehetetlenségi nyomatéka az alakváltozás irányában körülbelül 15%-kal nagyobb. Ez utóbbi adat miatt az lenne várható, hogy az 54E2 sínekkel szerelt vágánymező merevebb a hajlítóvizsgálatok során, azonban ennek éppen az ellenkezője igaz.
A megállapított E×I hajlítómerevségből helyettesítő inerciaértéket (I*) úgy lehet számítani, ha azt elosztjuk az acél E rugalmassági modulusával. A valóságban azonban ez nem pontos eljárás, mert a vágányt alkotó különböző anyagok kombinációja minden bizonnyal más modulusértéket eredményezne [6].
A manapság sokat idézett [7] irodalom 60E1 sínszálakkal, B70w vasbeton aljakkal, közvetlen sínleerősítésekkel szerelt vágányra I*=2,200×107 mm4 értéket ad meg, azonban a meghatározás módja (mérés, számítás) nem ismert. A [8] kutatási szakcikkben leírtak szerint ez a helyettesítő inerciaérték nem lehet helyes. „Ugyanis a két 60E1 rendszerű sínszál függőleges tengelyre vett inercianyomatéka 2Iy=1,026×107 mm4, ami azt jelenti, hogy a vágány megadott oldalirányú helyettesítő inerciája 114%-kal nagyobb, mint a csak síneket figyelembe vevő érték (2,2×107/1,026×107=2,144). A vágánykeretnek köszönhető óriási merevségnövekedés nem áll összhangban azzal a ténnyel, hogy a vágány hosszirányú ágyazat-ellenállása gyakorlatilag megegyezik az oldalirányú ellenállással. Ebből az következik, hogy az oldalirányú hajlítási merevség nem járul hozzá jelentősen a vágány oldalirányú ellenállásához, amit szinte teljes mértékben az ágyazat biztosít. Valójában az Amerikai Vasútmérnöki és Karbantartási Társulás (AREMA) szerint a hosszirányú terhelést a hézagnélküli sínek hőereje és az ágyazat belső súrlódásából adódó ellenállás eredője adja. Dogneton (Dr. Ing. Pierre Dogneton, Technical Counselor, Office for Research and Experiments [ORE]) kimutatta, hogy 23 tényező befolyásolja az oldalirányú vágányellenállást és megemlítette, ebben az aljtávolságnak alig vagy egyáltalán nincsen szerepe. Zarembski (Allan Zarembski, Professor of Practice, University of Delaware) szintén összeállított egy listát az oldalirányú elmozdulással szembeni ellenállást befolyásoló 23 tényezőből és ebből a listából az aljtávolság kizárásra került. Logikusan a vágányrács nem befolyásolhatja jelentősen az ágyazati ellenállást, ha azt az aljak távolsága nem befolyásolja. A vágányszerkezet 5-10%-kal járul hozzá az oldalirányú ellenálláshoz.”
A fenti megállapításhoz hasonló már jóval korábban, a [9] irodalomban is megjelent: „…a helyettesítő merevség értéke … a két sínszál saját (E×I)=E×2Isín merevsége sokszorosának adódott. Így a kivetődési számítások irreálisan magas értéket adtak a biztonság rovására. Kiderült, hogy az állandó nagyságú helyettesítő tehetetlenségi nyomaték vagy merevség feltételezése hibás, mivel a vágány nem egyetlen tömör gerenda.”
Az eddigiekben leírtak alapján kijelenthető, hogy egységesített vizsgálati paraméterek hiányában meglehetősen bizonytalan az állékonysági számításokhoz a szakirodalomban ismertetett értékek közül a korrekt oldalirányú inercia nagyságának megválaszthatósága.

A Nemesdy-féle számítási módszer

Dr. Nemesdy Ervin az 1960-as évek elején publikálta vágánystabilitási számítását. Elmélete szerint az oldalirányú kivetődéssel szemben három hatás dolgozik:
– a két sínszál vízszintes síkú saját merevsége E×I=E×2×Isín y,
– a sínleerősítések Mo elforgás-ellenállásából származó keretmerevségi hatás,
– az ágyazat q oldalirányú ellenállása.
A két végén befogott egyenes rúd (5. ábra) [9] esetében az Euler-féle kihajlási elmélet alapján a kritikus nyomóerő nagysága: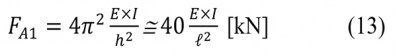

A sínszelvény merevségét és az elforgás-ellenállási állandóval jellemzett keretmerevségi hatást figyelembe vevő rugalmas vonal elemi differenciálegyenlete segítségével a kihajlást okozó nyomó­erő értéke:

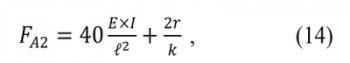ahol:
r = elforgás-ellenállási állandó [kNm/rad],
k = aljtávolság [m].
Az ágyazat oldalellenállásának értelmezése két végén befogott rúdnál a 6. ábra szerinti, a fekvéshibaalak közelítő parabolákból van összetéve [9]. Az ábrán láthatóan a hőerő kifelé mutató   R = 2×Fq×sinα eredőjével a Q=3/4×ℓ×q ágyazati oldalellenállás tart egyensúlyt.
Egyenes vágánygeometria esetén az A jelű, ℓ és f paraméterekkel jellemzett fekvéshibánál a kivetődést okozó kritikus nyomóerő képlete: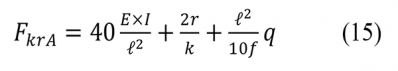

Az íves vágány esetére vonatkozó képletek az egyenes vágányra kidolgozott számítási kifejezések átalakításával jöttek létre. R sugarú íves geometria esetén a q ágyazati oldalellenállásnak már csak egy q–F/R nagyságú maradék része hatékony a stabilitás megőrzése érdekében. Ezért a 15. képlet így módosul:

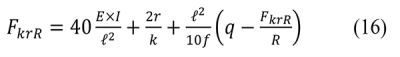Az íves vasúti vágány esetén a legkisebb kritikus erő értéke így számítható:

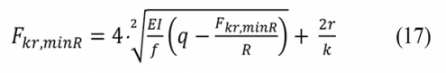A gyakorlatban nincsen olyan vágány, amelynek sínszálai tökéletes geometriával feküdnének. Az ívekben veszélyes A jelű, félhullám alakú irányhibát számításainkban az R sugarú vágánytengelyvonalra adjuk meg, ahogyan az a 7. ábrán látható. A hullámhossz nagysága ℓ, a kezdeti hiba húrmagassága f. Amennyiben adott körülmények között az irányhiba amplitúdója eléri a kritikus értékét (fkr), és a sínszálakban keletkező nyomóerő az ellenállásoknál nagyobbra nő, akkor bekövetkezik a kivetődés.